Qué Es El Volumen Y Cuál Es Su Fórmula

El volumen es una magnitud física que refleja la cantidad de espacio que ocupa un objeto. En otras palabras, es la medida tridimensional de un cuerpo, ya sea sólido, líquido o gaseoso. Para calcular el volumen de diferentes formas geométricas, se utilizan fórmulas específicas que dependen de la forma del objeto en cuestión.

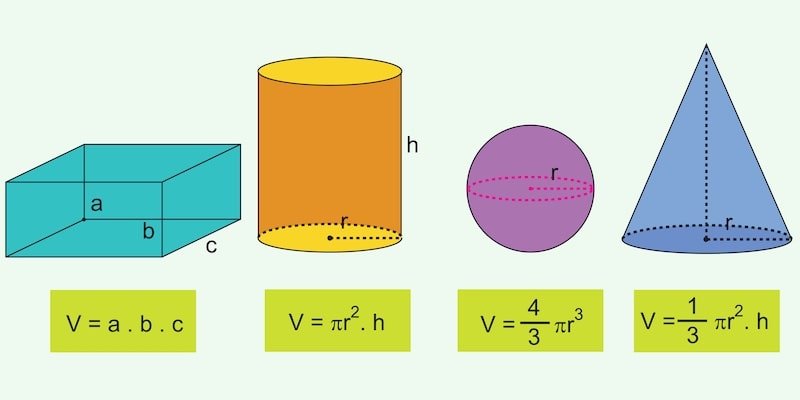
Fórmulas para calcular el volumen de algunas figuras geométricas:

Para un cubo: El volumen de un cubo se calcula elevando al cubo la longitud de uno de sus lados. La fórmula es V = L^3, donde V es el volumen y L es la longitud de un lado.
Para una esfera: El volumen de una esfera se calcula utilizando la fórmula V = (4/3) * π * r^3, donde V es el volumen, π es una constante aproximadamente igual a 3.14159, y r es el radio de la esfera.
Para un cilindro: El volumen de un cilindro se calcula multiplicando el área de la base por la altura. La fórmula es V = π * r^2 * h, donde V es el volumen, r es el radio de la base y h es la altura del cilindro.

Es importante recordar que el volumen se expresa en unidades cúbicas, como cm^3, m^3, etc. Calcular el volumen de un objeto es fundamental en diversas áreas, como la física, la química, la ingeniería y la arquitectura, ya que permite determinar la cantidad de espacio que ocupa un objeto y realizar cálculos relacionados con su capacidad, densidad, entre otros aspectos.

Definición y concepto básico del volumen

El volumen es una magnitud tridimensional que indica cuánto espacio ocupa un objeto. En otras palabras, es la cantidad de espacio que está ocupando un cuerpo en el espacio. En el contexto de la geometría, el volumen se refiere al tamaño de un objeto en tres dimensiones, ya sea un cubo, una esfera, un cono o cualquier otra figura geométrica.

Para calcular el volumen de diferentes formas geométricas, se utilizan fórmulas específicas que varían según la figura en cuestión. Por ejemplo, la fórmula para el volumen de un cubo es V = a^3, donde «a» representa la longitud de un lado del cubo. Para una esfera, la fórmula del volumen es V = (4/3)πr^3, donde «r» es el radio de la esfera.

Ejemplos de cálculo de volumen

Imaginemos que queremos calcular el volumen de un cilindro con radio de 5 cm y altura de 10 cm. Para ello, utilizamos la fórmula del volumen del cilindro, que es V = πr^2h. Sustituyendo los valores, obtenemos:

Radio (r) = 5 cm
Altura (h) = 10 cm

Cuántos litros lleva un m3 de agua

Por lo tanto, el cálculo del volumen sería:

V = π x 5^2 x 10 = 250π cm³

Otro ejemplo común es el cálculo del volumen de una pirámide. Si conocemos la base de la pirámide y su altura, podemos utilizar la fórmula V = (1/3) x base x altura para encontrar el volumen.

Calcular el volumen de diferentes objetos y figuras geométricas es fundamental en campos como la arquitectura, la ingeniería, la física y la química. Comprender cómo se calcula el volumen de un objeto ayuda a determinar su capacidad, su densidad o incluso a diseñar estructuras más eficientes.

La fórmula general para calcular el volumen

El volumen es una magnitud física que cuantifica el espacio ocupado por un objeto o una sustancia. Para calcular el volumen de diferentes formas geométricas, se utilizan fórmulas específicas que varían según la figura en cuestión. Sin embargo, existe una fórmula general que puede aplicarse a distintas situaciones para determinar el volumen de un objeto tridimensional.

La fórmula general para calcular el volumen de un objeto tridimensional es la siguiente:

Volumen = A x h

Donde:

A representa el área de la base del objeto.
h es la altura o la distancia perpendicular entre las bases en el caso de un objeto con forma de prisma o cilindro.

Esta fórmula es de gran utilidad cuando se trata de calcular el volumen de cuerpos geométricos simples, como prismas, cilindros, pirámides, conos, entre otros. Al conocer el área de la base y la altura del objeto, es posible aplicar esta fórmula de manera directa y obtener el volumen de forma rápida y precisa.

Por ejemplo, si tenemos un cilindro con un radio de 3 cm y una altura de 5 cm, podemos calcular su volumen de la siguiente manera:

Volumen = π x r² x h

Volumen = π x 3² x 5

Volumen ≈ 141,37 cm³

Por lo tanto, el volumen del cilindro sería aproximadamente 141,37 cm³.

Es importante recordar que esta fórmula general es de gran ayuda en situaciones donde se requiere calcular el volumen de formas simples, pero para figuras más complejas o irregulares, es necesario recurrir a fórmulas específicas o métodos alternativos de cálculo.

Aplicación de la fórmula del volumen en diferentes figuras geométricas

La fórmula del volumen es una herramienta matemática fundamental para calcular el espacio ocupado por un objeto en tres dimensiones. Esta fórmula varía según la figura geométrica de la que se trate, lo que nos permite determinar el volumen de diferentes objetos de manera precisa.

Por qué en algunas playas el agua es cristalina

1. Volumen de un cubo

Para un cubo, cuyas caras son todas iguales y perpendiculares entre sí, la fórmula del volumen es sencilla:

Volumen = Lado * Lado * Lado

Donde el lado representa la longitud de una de las aristas del cubo. Por ejemplo, si tenemos un cubo con aristas de 5 cm de longitud, su volumen sería:

Volumen = 5 cm * 5 cm * 5 cm = 125 cm³

2. Volumen de una esfera

Para una esfera, cuya forma es completamente redonda, la fórmula del volumen es:

Volumen = 4/3 * π * Radio³

Donde el radio es la distancia desde el centro de la esfera hasta cualquier punto de su superficie. Por ejemplo, si tenemos una esfera con radio de 3 cm, su volumen sería:

Volumen = 4/3 * π * 3³ = 113,1 cm³

3. Volumen de un cilindro

Para un cilindro, que consta de dos bases circulares paralelas, la fórmula del volumen es:

Volumen = π * Radio² * Altura

Donde el radio es la distancia desde el centro de la base circular hasta su borde, y la altura es la distancia entre las dos bases. Por ejemplo, si tenemos un cilindro con radio de 2 cm y altura de 6 cm, su volumen sería:

Volumen = π * 2² * 6 = 24π cm³ ≈ 75,4 cm³

Como podemos ver, la fórmula del volumen nos permite calcular de forma precisa la cantidad de espacio que ocupa un objeto en el espacio tridimensional, lo que resulta fundamental en campos como la arquitectura, la ingeniería, la física y muchas otras disciplinas.

Importancia y aplicaciones prácticas del cálculo del volumen

Una vez que hemos comprendido qué es el volumen y cómo calcularlo, es fundamental entender la importancia y las múltiples aplicaciones prácticas que tiene en diversas áreas. El volumen es una medida tridimensional que nos permite cuantificar el espacio ocupado por un objeto o una sustancia. Conocer el volumen de diferentes formas geométricas no solo es útil en matemáticas, sino que también tiene aplicaciones directas en la vida cotidiana y en diversos campos profesionales.

Aplicaciones prácticas del cálculo del volumen:

Arquitectura y construcción: En arquitectura, el cálculo del volumen es esencial para determinar la cantidad de material necesario para la construcción de edificaciones, como concreto, madera o vidrio. Además, permite estimar la capacidad de espacios interiores y planificar de manera eficiente el diseño de una estructura.
Ingeniería: En ingeniería, el cálculo del volumen es fundamental para el diseño de maquinaria, tanques de almacenamiento, tuberías, entre otros. Conocer el volumen de fluidos o materiales en un sistema es crucial para garantizar su correcto funcionamiento y seguridad.
Medicina: En el campo de la medicina, el volumen se utiliza para determinar la dosificación de medicamentos, la capacidad pulmonar de un paciente, el volumen sanguíneo circulante, entre otros aspectos clínicos relevantes para el diagnóstico y tratamiento de enfermedades.

Cuántos metros tiene la lanzadera de Aquarama

Estos son solo algunos ejemplos de cómo el cálculo del volumen es una herramienta fundamental en diversas disciplinas. Dominar este concepto no solo amplía nuestro conocimiento matemático, sino que también nos permite resolver problemas cotidianos y profesionales de manera más eficiente y precisa.

Preguntas frecuentes

¿Qué es el volumen y por qué es importante?

El volumen es la cantidad de espacio tridimensional que ocupa un objeto. Es importante porque nos permite conocer la capacidad de un objeto o sustancia.

¿Cuál es la fórmula para calcular el volumen de un cubo?

La fórmula para calcular el volumen de un cubo es V = a^3, donde «a» es la longitud de un lado del cubo.

¿Cómo se calcula el volumen de un cilindro?

El volumen de un cilindro se calcula con la fórmula V = πr^2h, donde «r» es el radio de la base y «h» es la altura del cilindro.

¿Cuál es la unidad de medida más común para el volumen?

La unidad de medida más común para el volumen es el metro cúbico (m³) en el sistema métrico.

¿Qué es la densidad y cómo se relaciona con el volumen?

La densidad es la cantidad de masa por unidad de volumen. Se relaciona con el volumen, ya que la densidad se calcula dividiendo la masa entre el volumen.

¿Cuál es la importancia de conocer el volumen en la vida cotidiana?

Conocer el volumen es importante en la vida cotidiana para actividades como cocinar, medir líquidos, diseñar objetos y en la construcción, entre otros.